曲柄摇杆机构的模拟仿真（Python）

本文讲述了关于如果使用 python，实现对曲柄摇杆机构（含双曲柄，双摇杆和以摇杆为主动件的尚未完成）的模拟仿真。如有大佬，望不吝赐教，感谢！

实现原理

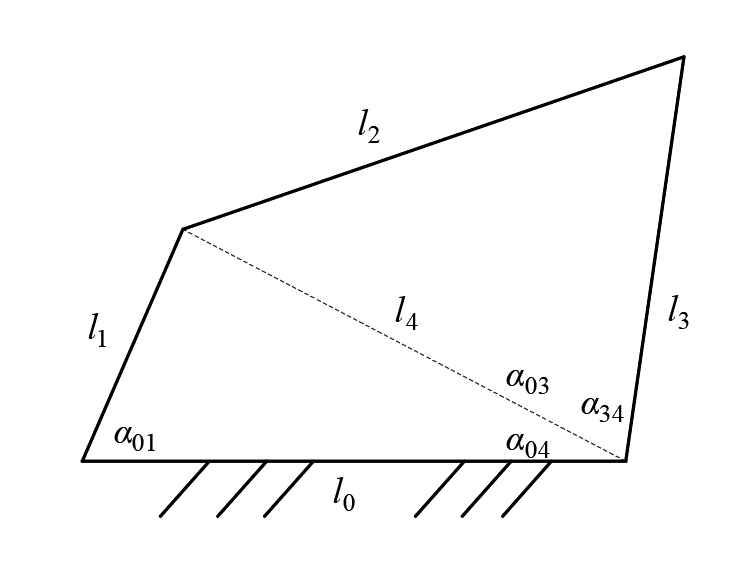
如图所示，$l_{0}$ 为机架，$l_{1}$ 为主动件，$l_{2}$ 为连杆，$l_{3}$ 为从动件，${\alpha_{01}}$ 为主动件旋转角度。可在任意时刻作辅助线 $l_{4}$，根据余弦定理可计算得出
$$l_4=\sqrt[2]{l_0^2+l_1^2-2l_0l_1\cos{\alpha_{01}}}$$
同理可得 ${\alpha_{04}}$ 和 ${\alpha_{34}}$。值得注意的是，${\alpha_{03}}$ 的计算分为两种
$${\alpha_{03}}=180^\circ-({\alpha_{34}}+{\alpha_{04}})\ , {\alpha_{01}}\leq180^\circ$$
$${\alpha_{03}}=180^\circ-({\alpha_{34}}-{\alpha_{04}})\ , {\alpha_{01}}>180^\circ$$
角度均以 $x+$ 方向起始。

代码

import math
import tkinter
import time

l0 = 90    #机架
l1 = 120   #主动杆
l2 = 95    #连杆
l3 = 110   #从动杆
n = 10     #转动圈数

# 判定
if min(l0,l1, l2, l3) + max(l0,l1, l2, l3) <= l0 + l1 + l2 + l3 - min(l0,l1, l2, l3) - max(l0,l1, l2, l3):
    if l0 == min(l0,l1, l2, l3):
        print('双曲柄机构')
    elif l2 == min(l0,l1, l2, l3):
        print('双摇杆机构')
    else:
        print('曲柄摇杆机构')
else:
    print('双摇杆机构')


root = tkinter.Tk()
root.title('曲柄摇杆模拟')
root.geometry('500x500')
root.resizable(0,0)

cv = tkinter.Canvas(root, width=500, height=300)
cv.pack()


# 原点 (80,100)
x0, y0 = 100, 150
cv.create_oval(x0-2,y0-2,x0+2,y0+2,fill='black')
# 机架
cv.create_line(x0,y0,x0+l0,y0,fill='black',width=3)
cv.create_oval(x0+l0-2,y0-2,x0+l0+2,y0+2,fill='black')

for a1 in range(360*n+1):
    # 删除之前的
    cv.delete('tmp')

    # 主动杆角度
    a1 = math.radians(a1)

    # 主动杆坐标
    x1 = l1 * math.cos(a1)
    y1 = l1 * math.sin(a1)
    # print('主动杆坐标：({},{})'.format(x1, y1))

    # 中间杆长
    l4 = l1**2 + l0**2 - 2*l0*l1*math.cos(a1)
    l4 = math.sqrt(l4)

    # 从动杆角度
    if abs((l0**2 + l4**2 - l1**2) / (2*l0*l4)) > 1:
        a04 = math.acos((l0**2 + l4**2 - l1**2) / (2.06*l0*l4))
    else:
        a04 = math.acos((l0**2 + l4**2 - l1**2) / (2*l0*l4))
    if abs((l3**2 + l4**2 - l2**2) / (2*l3*l4)) > 1:
        a34 = math.acos((l3**2 + l4**2 - l2**2) / (2.06*l3*l4))
    else:
        a34 = math.acos((l3**2 + l4**2 - l2**2) / (2.06*l3*l4))
    if math.degrees(a1) % 360 <= 180:
        a3 = math.pi - (a34 + a04)
    else:
        a3 = math.pi - (a34 - a04)

    # 从动杆坐标
    x3 = l3 * math.cos(a3) + l0
    y3 = l3 * math.sin(a3)
    # print('从动杆坐标：({},{})'.format(x3, y3))

    time.sleep(0.02)

    # 主动杆
    cv.create_line(x0,y0,x0+x1,y0-y1,fill='blue',tag='tmp',width=2)
    cv.create_oval(x0+x1-0.5,y0-y1-0.5,x0+x1+0.5,y0-y1+0.5,fill='black')
    # 连杆
    cv.create_line(x0+x1,y0-y1,x0+x3,y0-y3,fill='green',tag='tmp',width=2)
    # 从动杆
    cv.create_line(x0+l0,y0,x0+x3,y0-y3,fill='red',tag='tmp',width=2)
    cv.create_oval(x0+x3-0.5,y0-y3-0.5,x0+x3+0.5,y0-y3+0.5,fill='black')

    root.update()


root.mainloop()

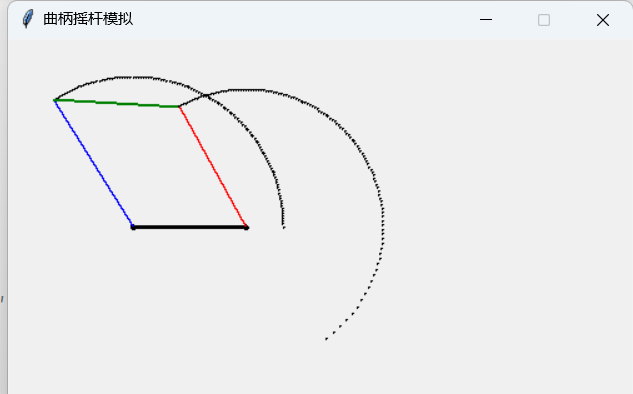
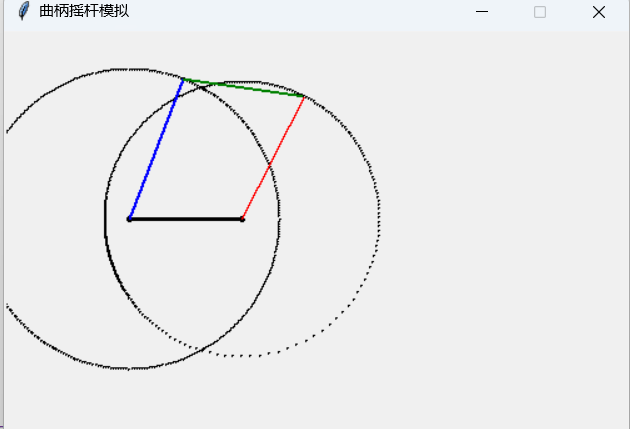
示例

小结

由于 python 的特性（浮点数精度保留），计算反余弦时有概率会报错，因为其值超出 [-1,1] 的区间了，网上也没什么特别好的方法，据说改调用 numpy 库会解决这一问题，但我想尽量使用自带库就没有尝试，后期可能会试一下，目前是使用判定，若超出范围，则对其值乘上 0.97（即代码中的值 2.06）使之强行落在范围内，所以在一些特定情形下会出现从动件 l3 跳跃和抖动。
值得注意的是 math 库中计算三角函数角度单位均为弧度（rad），这可能也是导致第 1 条的一个原因吧。
同样还是 python 自带库的问题，range 函数无法生成小数间隔的数列，所以目前最小分辨率是 1°，后期会自己写一个生成器或采用 numpy 库的。
暂时因为时间原因尚未完成双摇杆和以摇杆为主动件的模拟仿真，未来即将补上。
即将补上的还有完善 GUI 布局。
如果有大佬或者其他感兴趣的同志，欢迎和我联系 ([email protected])。
下载请见 Malvern’s File Server。

本文采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处，谢谢！